

This is a brief introduction, and tutorial, to high-power narrow-linewidth dispersive tunable laser oscillators. The multiple-prism grating oscillators described here yield single-longitudinal-mode emission (with laser linewidths in the sub GHz range) throughout the visible spectrum in near-Gaussian temporal pulses, a few nanoseconds long, at powers in the kW regime. These dispersive architectures are applicable to all-known tunable laser gain media in the gas, liquid, or solid state, including semiconductors (also known as diodes). Coherent emission from electrically-pumped organic semiconductor emitters is also described. ©
Note: also available: Understanding lasers in a few simple words.
Key words: beam divergence, diode lasers, coherence, coherent, course, courses, Dirac's notation, dispersion, dye lasers, electrical pumping, electrical excitation, electrically excited, gas lasers, grating, interferometric, instruction, laser, laser-cavity, lecture, linewidth, multiple-prism, organic laser, organic lasers, oscillator, polymer laser, polymer lasers, prism, prism compressor, prism compressors, pulse compression, pulse compressors, resonator, solid-state lasers, teaching, tunable, tunability, tuning.
Tunable lasers are different to traditional lasers because they can continuously change their emission wavelength, or color, in a given spectral range. As such, these quantum devices have found numerous applications in many diverse fields. In particular, tunable lasers have played a crucial and sustained role in advancements of fundamental physics and science. Among basic fields that employ tunable lasers are


.jpg)
Applied fields that employ tunable lasers include
Tunable lasers were discovered by Sorokin and Lankard [10] and Schäfer et al. [11] in 1966. This was the dye laser. At first, the radiation from these organic lasers was in the form of broadband emission. Broadband emission is generally comprised by several transverse modes and a multitude of longitudinal modes in each transverse mode. An important advance towards emission control was provided with the invention of the continuous wave dye laser by Peterson et al. [12] in 1970. In the area of high-power pulsed dye lasers a significant improvement was the introduction of the telescope-grating oscillator by Hänsch [13] in 1972. This telescopic cavity introduced expansion of the intracavity beam illuminating the diffraction grating. However, the telescopic cavity was not compact and required a large two-dimensional diffraction grating.
Resonator laser architectures that yield tunable narrow-linewidth emission in compact, simplified, and improved configurations are the grazing-incidence grating cavities [14-16] and the multiple-prism grating oscillators [10-12]. The multiple-prism grating oscillators include the multiple-prism Littrow (MPL) grating cavities and the hybrid multiple-prism near-grazing-incidence (HMPGI) grating cavities [16-18]. These cavity architectures have been also successfully applied to wavelength tuning and frequency narrowing in gas lasers, solid-state lasers, and semiconductor lasers [20-23]. The physical, and technological, features of various broadly tunable gain media are reviewed in [24-26]. Here we list the approximate tuning range of some representative broadly tunable lasers:
Additional tunable sources of coherent radiation include the optical parametric oscillators (OPOs) and the free electron laser [25]. Both these alternative sources of coherent radiation do not depend on the process of population inversion to generate coherent emission [26].
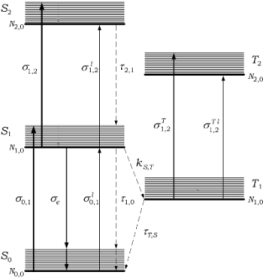
In order to illustrate the principle of tunability we consider a typical laser dye molecule with a corresponding energy diagram as illustrated in Fig. 1. Dye molecules are very large, typically with molecular weights in the 300-600 mu range, with a multitude of overlapping energy levels. In the energy diagram of Fig. 1 each of the electronic states of the molecule (S0... S2) contains a manifold of overlapping vibro-rotational levels (denoted by the fine horizontal lines at each electronic state).
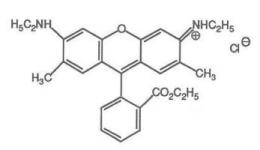
The laser dye molecule rhodamine 6G is depicted in Fig. 2.

In the following description, which ignores triplet states, it is necesary to remember that energy differences are related to frequency differences via Planck's quantum energy equation. In Fig. 1, the ground electronic state is S0 and the first excited state is S1. Molecules are excited from the ground state to either S1 or S2. If excited to S2 the molecules rapidly decay, in a radiationless manner, to S1. From the lower level of S1 transitions can take place to any level at the ground state manifold. It is this energy decay range that gives origin to tunability. This is explained in greater details, with corresponding equations, in [16]. Initially organic lasers used a liquid gain medium where the organic dye molecules are diluted in a solvent such as ethanol or methanol [1-3]. In a solid-state dye laser the organic dye molecules are uniformly distributed in a highly homogenous polymer matrix. In a tunable polymer laser the gain medium is said to be a dye-doped polymer. An example of such polymer is a highly pure form of poly(methyl-methacrylate) (PMMA).
In the case of semiconductor gain media, or diode gain media, the tunability range depends approximately on the separation of the conduction and the valence bands, minus the energy band gap, of the semiconductor.
In order to make a tunable laser the first element needed is a laser gain medium with a broad gain profile. Once broadband laser emission is achieved in a simple mirror-mirror cavity, lasing must be restricted to a single-transverse mode (TEM00) using a suitable intracavity aperture. Once lasing is restricted to a TEM00 mode then one can proceed to limit emission to a single longitudinal mode (SLM). This is done via the introduction of suitable dispersive elements, such as prisms, gratings, or a combination of these. The dispersive resonator assemblies can provide a very narrow window for intracavity transmission in the frequency domain. A well designed multiple-prism grating assembly can restrict oscillation to a SLM. Wavelength tuning is generally achieved by rotation of either a grating or a mirror.
It can be shown that laser linewidth is directly proportional to the beam divergence and inversely proportional to the overall intracavity dispersion [1, 12, 26-31]. Hence, once lasing has been restricted to a TEM00 emission, the main concept in linewidth narrowing consists in reducing the beam divergence towards its diffraction limit and, at the same time, multiplying the angular dispersion provided by the diffraction grating [1, 27, 28, 30-32]. The intracavity dispersion available from a suitable grating can be augmented substantially, up to 100 times or more, by multiple-prism expansion of the laser beam emitted at the gain medium
in order to illuminate the whole grating [30, 31]. A multiple-prism grating cavity is illustrated in Fig. 3.

A detailed discussion of the physics of linewidth narrowing, in tunable lasers, is given by Duarte [1, 8, 23, 30, 34]. The concepts outlined above can be summarized in the linewidth equation [PDF] given elsewhere [1, 23]. This cavity linewidth equation can be derived from interferometric quantum principles via Dirac's quantum notation [16, 25, 27]. The equation for the beam divergence can be established directly from the uncertainty principle [1, 8, 23, 35].
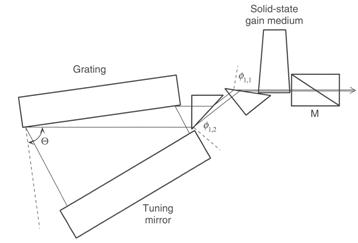
The generalized linewidth and dispersion theory of multiple-prism grating oscillators is given elsewhere [1, 8, 23, 30-32, 36]. This theory is also applicable to prismatic pulse compression, and prism pulse compressors, in femtosecond lasers [23, 37-39]. Figure 4 depicts a basic intracavity two-prism compressor in a femtosecond laser cavity. At this stage it should be clarified that multiple-prism arrays can be configured, at will, to either yield very high intracavity dispersion, very small intracavity dispersion, or even substract dispersion. Very large intracavity dispersion, achieved using multiple-prism grating configurations (see Fig. 3), is necessary to obtain very narrow linewidth emission [15]. On the other hand, very small intracavity dispersion, achieved using prismatic configurations as depicted in Fig. 4, leads to very broadband emission and hence to pulse compression.
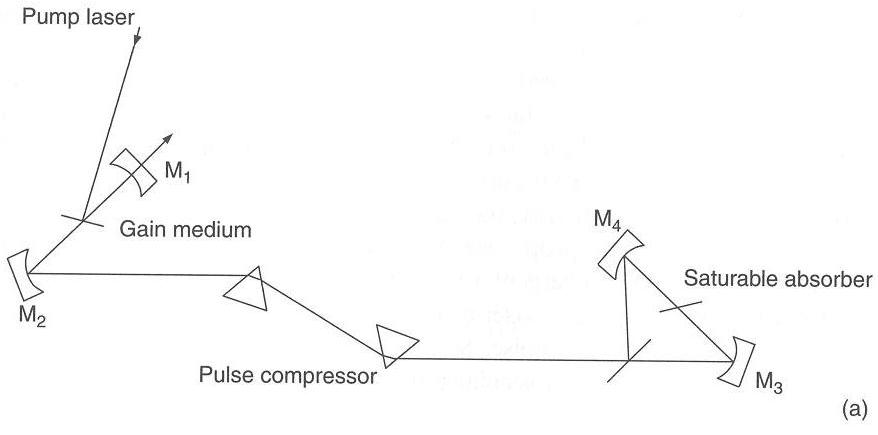
Although liquid dye lasers have been very successful, and extraordinarily pervasive, there has been an effort to find new gain media in the solid-state that would simplify the engineering of this class of lasers. The gain media used in these lasers are organic dye-doped polymers. The first narrow-linewidth solid-state dye laser oscillators [39] were reported in 1994. Shortly thereafter emission characteristics were improved and single-longitudinal-mode emission, in a near Gaussian temporal pulse, was reported [41, 42]. Here the optical architecture of these tunable oscillators is described.
Figure 5 illustrates an optimized hybrid multiple-prism near grazing-incidence (HMPGI) grating solid-state dye laser oscillator [43].
This oscillator has a cavity length of 73 mm and yields a laser beam with a TEM00 profile and a divergence ~ 1.5 times the diffraction limit. The oscillator lases in a single-longitudinal-mode at a linewidth of 375 MHz. The tuning range is 565-610 nm. The temporal emission is in a near-Gaussian pulse 7 ns (FWHM) in duration and its conversion efficiency is 3-4%. This oscillator is excited longitudinally. HMPGI oscillators were first introduced in the development of narrow-linewidth copper-vapor-laser pumped dye lasers [11] which have been successful in applications for laser isotope separation and the nuclear industry. A photograph of such laser oscillator is shown in Fig. 6.

One of the narrow-linewidth solid-state dye laser oscillators introduced in 1994 is shown in Fig. 7. This particular configuration includes a three-prism beam expander and a grating in Littrow configuration [34].

An optimized solid-state multiple-prism Littrow (MPL) grating dye laser oscillator [44] is depicted in Fig. 8.
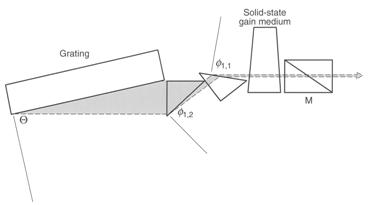
This is an optimized oscillator architecture with a cavity length of 75 mm. The angle of incidence at the grating, deployed in Littrow configuration, is about 77 degrees. This cavity yields a laser beam with a TEM00 profile and a divergence 1.5 times the diffraction limit. This oscillator lases in a SLM at a linewidth of 350 MHz. The tuning range is 550-603 nm. The temporal emission is in a near-Gaussian pulse 3 ns (FWHM) in duration and its conversion efficiency is 5%. Excitation is longitudinal to the optical axis of the cavity [44]. This relatively efficient narrow-linewidth performance is made possible by the robust broadband efficiency of solid-state polymeric dye lasers which is reported to be, rather conservatively, in the 40-60% range [39, 44].
A laser linewidth of 350 MHz corresponds to about 0.0004 nm at a wavelength of 590 nm. It should be noted that a typical Doppler-linewidth for single-rotational transitions, in many types of molecules, is in the 1 to 2 GHz range. A lasing performance characterized by a linewidth of 350 MHz and a Gaussian temporal pulse length of 3 ns (FWHM) is near the limit allowed by Heisenberg's uncertainty principle.
The interesting feature of this optimized MPL grating architecture is that it fully utilizes the dispersive capability of a higher density diffraction grating, at a higher angle of incidence, thus reducing the requirements on beam expansion and cavity length needed to achieve a laser linewidth similar to that obtained with HMPGI grating cavities [44]. To date this is the narrowest laser linewidth reported for solid-state dye laser oscillators.
The type of emission available from these tunable solid-state
multiple-prism grating oscillators is characterized by smooth TEM00 beam
profiles (shown in Fig. 9)

and clean single-longitudinal-mode emission as illustrated by the Fabry-Perot interferogram shown in Fig. 10.

This performance was achieved at extremely low amplified spontaneous emission (ASE) levels. Very low ASE levels (that is, very low quantum noise levels) are characteristic of well designed laser oscillators with "closed cavity" configurations [1, 16-18, 22, 29] as illustrated in Figs. 5-8. This is particularly attractive when one considers that laser emission is available throughout the visible spectrum at pulses in the kW regime.
The lasers described up to this point are optically pumped, that is, they use indirect electrical excitation. In the next section tunable lasers using direct electrical excitation of the gain medium are described.
A more subtle issue concerning tunable laser oscillators is the class of cavity being employed. These can be divided between open and closed cavities [29]. Open cavities couple the output emission via reflection or diffraction losses. As such, they are vulnerable to interaction with extra-cavity optical elements. Closed cavities, on the other hand, couple the output emission via transmission of an output mirror or mirror-polarizer element [40-44]. Closed cavities yield better signal-to-noise ratios, than open cavities, and offer protection against unwanted external optical feedback. This is very important to ensure, and maintain, stable very narrow-linewidth emission for applications susch as laser cooling. The usual "open cavity" diode-laser oscillators require the use of optical isolators to protect the cavity from unwanted optical coupling.
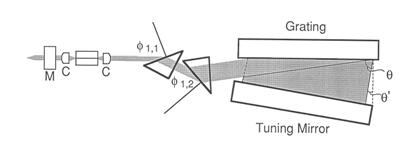
Fig. 11 Closed-cavity multiple-prism near grazing-incidence grating configuration for tunable diode lasers (from [20, 46]) .
HMPGI and MPL grating oscillator architecures are used with a variety of tunable laser gain media in the gas, the liquid, and the solid state. Indeed, their versatility has been amply demonstrated from compact tunable semiconductor lasers [1, 20-23, 46] to powerful pulsed gas lasers [47, 48]. Multiple-prism grating and multiple-prism near grazing-incidence grating oscillator configurations for high-power CO2 lasers are shown in Fig. 12, and Fig. 13, respectively.


Comprehensive theoretical and experimental reviews on this subject are given in Tunable Lasers Handbook [26]. Further applications are discussed in Dye Laser Principles [25] and Tunable Laser Applications [49-51].

The second enlarged edition of Tunable Laser Applications discusses spectroscopic applications of optical parametric oscillators and tunable diode lasers as well as medical applications of organic dye lasers, fiber lasers, and crystalline solid state lasers. In particular, specific designs to build tunable narrow-linewidth diode lasers yielding intrinsic circular beams are discussed in Chapter 5 of [50, 51]. In the 3rd edition of Tunable Laser Applications applications discussed in detail include tunable laser isotope separation (LIS), imaging, interferometry, and laser microscopy. In regard to LIS, the use of high-power tunable narrow-linewidth lasers for uranium and lithium LIS is discused in a Chapter 11 which is entitled Tunable laser atomic vapor laser isotope separation.
Interest in electrically-pumped organic lasers goes back to the mid 1970s [52, 53]. Coherent emission from electrically excited organic semiconductor interferometric emitters was reported, for the first time, by Duarte et al. [54] in 2005. The emission medium is the laser dye coumarin 545 tetramethyl [55, 56] in a tandem OLED architecture. A study on the emission characteristics of the electrically-excited organic semiconductor interferometric emitter has been reported by Duarte [57]. The emission is characterized by a nearly diffraction limited near -Gaussian beam (1.09 X diffraction limit), and high visibility (V = 0.9) interferograms. The interferograms exhibit the high-visibility typical of interferograms corresponding to laser radiation. In other words, the emission from these sub-micrometer resonators, within an interferometric structure, is found to be spatially coherent and spectrally indistinguishable from the emission corresponding to pulsed dye lasers [9, 10]. A striking feature of this radiation is that, due to the nanocavity length involved, the emission inherently corresponds to a single-longitudinal-mode [50]. Hence, as far as coherence is concerned, the emission of this electrically-pumped dye-doped organic interferometric emitter is indistinguishable from laser emission. A discussion on the coherence properties of this organic semiconductor emission is given in [58, 59, 60]. More recently, this emission has been associated with intrinsic quantum coherence (see Note 13).

Electrical excitation was performed using ns risetime pulses, usually ~ 100V/pulse, and into the kV/pulse excitation regime[57]. Subsequent experiments from electrically-pumped organic devices have been reported by Liu et al. [61]. These authors use only a single gain region, a similar experimental configuration, and also a tetramethyl-type dopant. They report very similar results with interferogram visibilities of V = 0.89 at ~ 622 nm. A detailed commentary on these results is given in [60].
A resource letter on coherent electrically-pumped organic semiconductor interferometric emitters is available in PDF.
Note 1: the amplification of tunable narrow-linewidth laser emission using master-oscillator forced-oscillator configurations is described in [62].
Note 2: in addition to the dispersive narrow-linewidth dye lasers described here there has also been recent progress in the development of distributed feedback solid-state dye lasers [63, 64]. For a review on solid-state dye laser matrices the reader should refer to Costela et al. [65]. Recent progress on silicon-modified organic dye laser matrices is given by Costela et al. [66, 67] and a discussion on crosslinked polymeric networks is provided by Bañuelos Prieto et al. [68].
Note 3: recent work on external-cavity grazing-incidence grating semiconductor lasers involves de use of MEMS techniques to produce miniature resonators [69, 70].
Note 4: a detailed introduction to narrow-linewidth laser oscillators and wavelength-tuning techniques is given, at a textbook level, in Tunable Lasers Optics [1, 23]. This material is aplicable to both high-power tunable oscillators and miniature resonators. A discussion on longitudinal tuning techniques for miniature lasers is given in Chapter 7 of Tunable Laser Optics. These longitudinal techniques are particularly applicable to MEMS driven tuning and are further refined and discussed in Chapter 5 of Tunable Laser Applications, 3rd Edition.
Note 5: new tunable solid-state laser materials described as dye-doped polymer-nanoparticle gain media have been recently reported in the literature [71]. These gain media offer reduced dn/dT coefficients which allow the attainment of laser beam divergences approaching the diffraction limit. The silica nanoparticles are arranged, in a fairly uniform distribution, in the dye-doped polymer [72].
Note 6: a continuous-wave solid-state dye laser, using a rotating disc gain media configuration, has been reported by Bornemann et al. [73]. Laser linewidth, integrated over 20 ms, is reported to be ~ 0.5 nm at 580 nm (or 446 GHz). A second generation CW device is reported to yield time integrated linewidths of about 0.05 nm (~ 43 GHz) [74]. However, stable CW narrow-linewidth emission (analogous to liquid dye laser emission, see [75]) from a solid-state dye laser has not yet been reported.
Note 7: interesting recent developments on various photonic, nanobiophotonic, and non-linear optics properties of hybrid nanocomposite organic materials is given in [76, 77].
Note 8: the generalized multiple-prism theory has been extended, via an elegant mathematical framework, to any higher-order phase derivative [78].
Note 9: quantum cascade lasers (QCLs) are being tuned using external Littrow configurations [79] and MEMS techniques [80]. Micro cavities using folded Fabry-Perot geometries have also been reported [81].
Note 10: a recent review on organic-inorganic lasers id given by Costela et al. [82].
Note 11: A recent review on the generalized theory of multiple-prism pulse compression for femtosecond lasers is given in [83].
Note 12: The possible use of tunable coherent sources for the emission of multiple photon pairs, in multiple propagation channels, for quantum entanglement experiments is outlined in [84].
Note 13: The quantum origin of the coherent emission in the electrically-pumped organic semiconductor interferometric emitter [54] has been described as intrinsic quantum coherence [85].
.jpg)



First published on the 17th of December, 1999. Updated on the 17th of February, 2023.